Souborové formáty

Kurz počítačové grafiky

Vzorkování a kvantizace

Převod ze spojitého signálu na digitální
Příkladem je digitální fotoaparát:
- Vzorkování: 'spojitý' proud fotonů je zachytáván na 'mřížce' CCD čipu
- Kvantizace: 'spojité' hodnoty intenzity jednotlivých pixelech převáděny na konečný počet úrovní

Pixel

Zkratka picture element je jednak označení pro jeden bod rastrového obrázku a druhak je to jeden svítící bod na monitoru.

Jsou pixel na obrazovce a v rastrovém obrazu totožné?

Ne nutně. Je důležité si uvědomit, že jeden pixel na monitoru může vzniknout z více/méně pixelů rastrového obrázku.

Rozlišení

U tiskáren udáváno v jednotce DPI (dots per inch) a u monitorů v jednotce PPI (pixels per inch).

Je informace o rozlišení součástí souborů s rastrovým obrázkem?

Nikoliv. Mějte na paměti, že tento údaj má smysl udávat pouze u technických zařízení jako jsou tiskárny, kopírky, apod. Může se ovšem objevit v tzv. meta datech obrázků, které vznikly naskenováním.

Dynamický rozsah

Udává počet úrovní, který má jeden barevný kanál a je určen počtem bitů, který slouží pro uložení jednoho barevného kanálu.

Některé příklady ze života

1 bit: 2 úrovně (tzv. bitmapa)
8 bitů: 256 úrovní (úrovně šedi nebo barevná paleta)
12 bitů: 4096 úrovní (některé lepší digitální zrcadlovky)
16 bitů: 65 536 úrovní nebo half-float
32 bitů: float

Uložení barvy pomocí (s)RGB

K uložení barvy se musí použít nějaký konkrétní barevný prostor. Nejčastěji se používá barevný prostor sRGB. Méně často Adobe RGB.

Převod z XYZ do RGB lineární

$$ \begin{bmatrix} R_\mathrm{linear}\\G_\mathrm{linear}\\B_\mathrm{linear}\end{bmatrix}= \begin{bmatrix} 3.2406&-1.5372&-0.4986\\ -0.9689&1.8758&0.0415\\ 0.0557&-0.2040&1.0570 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} $$

RGB lineární

Výsledkem předchozího převodu jsou tzv. RGB lineární hodnoty, které jsou v rozsahu $ <0, 1> $

Hodnoty RGB lineární se používají při interním zpracování v počítači, ale pro uložení je často vhodné provést gamma korekci.

Gamma korekce

Používá se především z toho důvodu, že naše vnímání intenzity světla je značně nelineární.

$$ V_{out} = A V_{in}^{\gamma} $$

Gamma korekcí tudíž efektivně využíváme daný dynamický rozsah daného kanálu (8/16 bitů na kanál).

Převod z RGB lineární do sRGB (gamma korekce).

Pokud za C dosadíme jednotlivé barvy z RGB lineární, pak pro převod do sRGB platí vztah:

$$ C_\mathrm{srgb}=\begin{cases} 12.92C_\mathrm{linear}, & C_\mathrm{linear} \le 0.0031308\\ (1+a)C_\mathrm{linear}^{1/2.4}-a, & C_\mathrm{linear} > 0.0031308 \end{cases} $$

, kde $ a = 0,055 $

Převod z sRGB do RGB lineární

$$ C_\mathrm{linear}= \begin{cases}\frac{C_\mathrm{srgb}}{12.92}, & C_\mathrm{srgb}\le0.04045\\ \left(\frac{C_\mathrm{srgb}+a}{1+a}\right)^{2.4}, & C_\mathrm{srgb}>0.04045 \end{cases} $$

Převodní funkce (gamma korekce)

Gamut sRGB

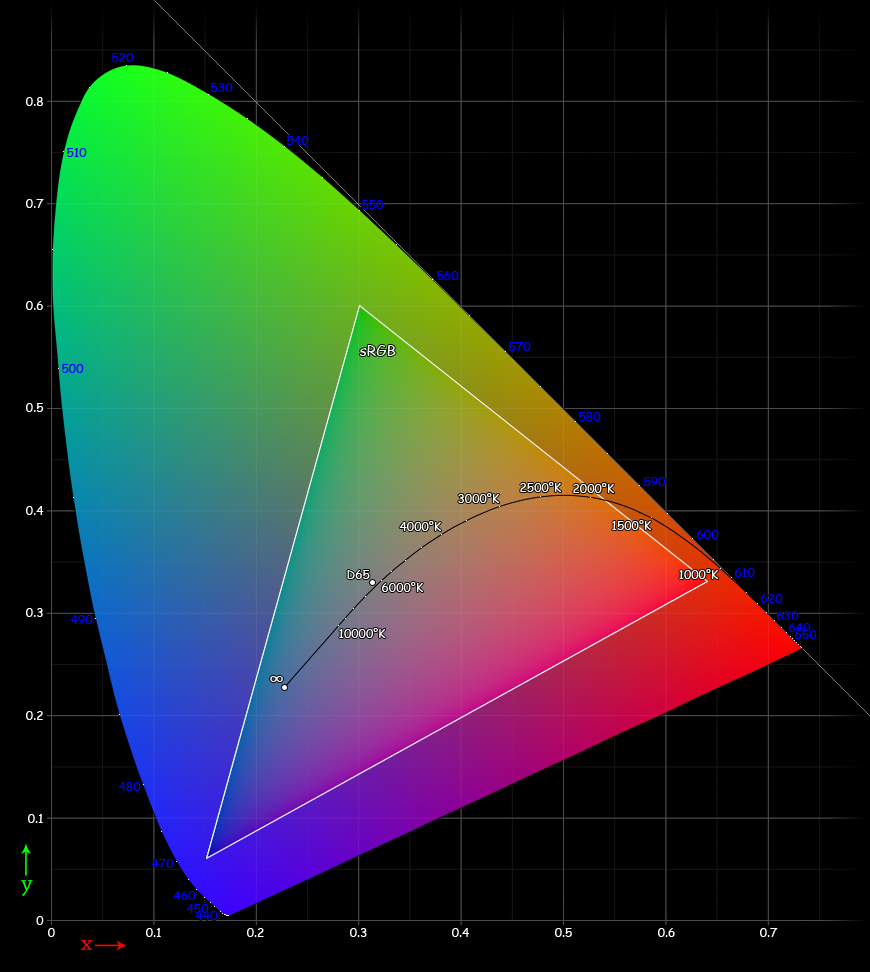
Alfa kanál

Určuje průhlednost každého pixelu. Konvence je taková, že hodnota 0 reprezentuje úplně průhledný pixel a maximální hodnota rozsahu (např.: 1.0 nebo 255) úplně neprůhledný pixel.

Barevná paleta

Některé souborové formáty umožňují vyjádřit barvu pixelu nikoliv přímo pomocí barvy, ale pomocí indexu do barevné palety.

Paleta bývá nejčastěji adaptivní (obsahuje maximum barev z původního obrázku).

Komprese obrazové informace

Rastrové obrázky mohou být skutečně velké. Z toho důvodu se pro jejich uložení používá jak bezeztrátová tak i ztrátová komprese.

Bezeztrátová komprese

RLE kódování
Huffmanovo kódování
LZW kódování
DEFLATE

Ztrátová komprese

Využívá nedokonalosti lidského oka, kdy je možné některé informace vypustit aniž bychom to poznali.

Vyšší citlivost na změnu jasu než na změnu barvy
Neschopnost rozlišit změny ve vysokofrekvenčním signálu

JPEG komprese

Jedná se o ztrátový kompresní formát, který je používan nejen v obrázcích z příponou .jpg/.jpeg (JFIF)

Nalezneme ho i v grafických formátech TIFF, PDF, PS, MOV, apod.

Je vhodná na komprimaci pouze některých obrázků: fotografií, naskenovaných dokumentů, které jsou ze své podstaty rozmazané.

Základní vlastnosti

Vytvořeno koncem 80. let Joint Picture Expert Group
Je možné použít 4 režimy činnosti, ale běžně jsou podporovány jenom první dva
- Sekvenční
- Progresivní
- Bezeztrátový
- Hierarchický

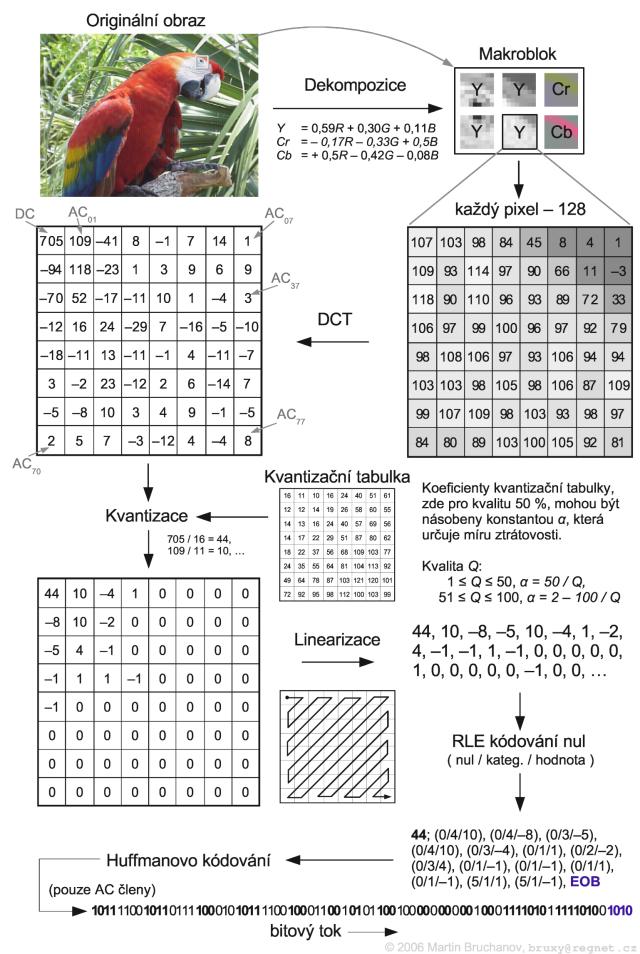
Kroky sekvenčního režimu komprese

Převod do barevného prostoru YCbCr
Převzorkování (4:4:4, 4:2:2)
Rozdělení obrázků do makrobloků
Diskrétní kosinová transformace (DCT)
Kvantizace pomocí kvantizační matice
Linearizace (Zig-Zag)
RLE kódování
Huffmanovo (Aritmetické) kódování

Převod z RGB (lineární) do YCbCr

Pokud jsou vstupní hodnoty (RGB) v rozsahu $ <0, 255> $, tak převod může mít následující podobu a výstupní hodnoty (YCbCr) budou v rozsahu $<-127, 127>$

$$ \begin{bmatrix} Y \\ C_{b} \\ C_{r} \\ 1.0\end{bmatrix}= \begin{bmatrix} 0.299 & 0.587 & 0.114 & 0.0 \\ -0.1687 & 0.3313 & 0.5 & -128 \\ 0.5 &-0.4187 &-0.0813& -128 \\ 0.0 & 0.0 & 0.0 & 1.0 \\ \end{bmatrix} \begin{bmatrix} R \\ G \\ B \\ 1.0 \end{bmatrix} $$

Převzorkování

Jelikož je lidské oko více citlivé na změnu jasu než na změnu barvy, tak je možné vynechat některé barevné vzorky.

Jasová složka je vždy zachována. Barevné složky jsou průměrovány z 2x2 pixelů nebo 2x1 pixelů. Tím dochází k první ztrátě informace.

Čím je způsobena větší citlivost lidského oka na jas než na barvu?

Je to dáno počtem tyčinek (120 mil.) a čípků (8 mil.).

Rozdělení obrazu do makrobloků

Každý převzorkovaný barevný kanál je rozdělen do makrobloků 8x8.

Diskrétní kosinová transformace (DCT)

Nejde o ztrátovou operaci. Pouze dojde k jinému vyjádření diskétních hodnot.

Pro jednorozměrný případ má následující podobu:

$$ X_k = c_{k} \sum_{n=1}^{N-1} s(n) \cos \frac{\pi(2n + 1)k}{2N} \quad k = 0, \dots, N-1. $$ $$ c_{k} = \begin{cases} \sqrt{1/N}, k=0\\ \sqrt{2/N}, k>0 \end{cases} $$

Diskrétní kosinová transformace (DCT)

Pro dvourozměrný případ má následující podobu a N má v našem případě (JPEG) hodnotu 8:

$$ X_{(i,j)} = c_{(i,j)} \sum_{n=1}^{N-1}\sum_{m=1}^{N-1} s(m,n) \cos \frac{\pi(2m + 1)i}{2N} \cos \frac{\pi(2n + 1)j}{2N} $$ $$ c_{(i,j)} = c_{i} c_{j} $$

Kvantizace pomocí kvantizační matice

Výstupem DCT je transformovaný makroblok 8x8 jeho hodnoty jsou podělené kvantizační maticí (50% komprese):

$$ \begin{bmatrix} 16 & 11 & 10 & 16 & 24 & 40 & 51 & 61 \\ 12 & 12 & 14 & 19 & 26 & 58 & 60 & 55 \\ 14 & 13 & 16 & 24 & 40 & 57 & 69 & 56 \\ 14 & 17 & 22 & 29 & 51 & 87 & 80 & 62 \\ 18 & 22 & 37 & 56 & 68 & 109 & 103 & 77 \\ 24 & 35 & 55 & 64 & 81 & 104 & 113 & 92 \\ 49 & 64 & 78 & 87 & 103 & 121 & 120 & 101 \\ 72 & 92 & 95 & 98 & 112 & 100 & 103 & 99 \end{bmatrix} $$

Kvantizace a komprese

Během kvantizace dochází k největší ztrátě dat.

Kvantizační matice může být vynásobena koeficientem a tím můžeme jednak určit kvalitu komprese ale i míru ztráty obrazové informace.

Kvalita komprese se udává většinou v procentech.

Příklad kvantizace

Pokud následující makroblok 8x8 (výsledek DCT)

$$ \begin{bmatrix} -415 & -33 & -58 & 35 & 58 & -51 & -15 & -12 \\ 5 & -34 & 49 & 18 & 27 & 1 & -5 & 3 \\ -46 & 14 & 80 & -35 & -50 & 19 & 7 & -18 \\ -53 & 21 & 34 & -20 & 2 & 34 & 36 & 12 \\ 9 & -2 & 9 & -5 & -32 & -15 & 45 & 37 \\ -8 & 15 & -16 & 7 & -8 & 11 & 4 & 7 \\ 19 & -28 & -2 & -26 & -2 & 7 & -44 & -21 \\ 18 & 25 & -12 & -44 & 35 & 48 & -37 & -3 \end{bmatrix} $$

Podrobýme kvantizaci kvantizační maticí, tak dostaneme následující makroblok:

$$ \begin{bmatrix} -26 & -3 & -6 & 2 & 2 & -1 & 0 & 0 \\ 0 & -3 & 4 & 1 & 1 & 0 & 0 & 0 \\ -3 & 1 & 5 & -1 & -1 & 0 & 0 & 0 \\ -4 & 1 & 2 & -1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$

Linearizace

RLE kódování

Run Lenght Encoding bezeztrátově komprimuje opakující se hodnoty. Princip jejího fungování si ukážeme na zjednodušeném příkladu. Mějme sekvenci hodnot:

V této sekvenci se několikrát opakuje hodnota 4, takže pokud si vhodně zvolíme speciální symbol (v našem případě to bude 0, protože se v původní sekvenci nevyskytuje) značící začátek komprimované sekvenci, tak komprimovaná sekvence může vypadat následovně:

Huffmanovo kódování

Hodnoty s vyšší frekvencí jsou kódovány kratším bitovým slovem než hodnoty s menší frekvencí.

Rastrové souborové formáty

Vybrané souborové formáty pro uložení rastrové grafiky: TGA, BMP, GIF, PNG, JFIF (JPEG), TIFF, WebP, OpenEXR

Existují samozřejmě mnohé další: PCX, XBM, XPM, PPM, PBM, APNG, JPEG 2000, BPG, MNG, HDR, atd.

Targa Truevision (TGA)

“Keep It Simple, Stupid!”

Vlastnosti TGA

Bitmapa (1bpp)
Barevná paleta (8bpp) RGB
256 odstínů šedi (8bpp)
RGB (24bpp), RGBA (32bpp)
Volitelně RLE komprese

BMP

“Be on web or die!”

Vlastnosti BMP

Vytvořil Microsoft a IBM
Pixmapa (1bpp)
Omezená barevnost
- 16 barev (4bpp)
- 256 barev (8bpp)
- 65 536 barev (16bpp)
RGB (24bpp)
Barevná paleta
Volitelně RLE komprese, která někdy obrázky zvětšovala

GIF

“Animated gifs all around!”

Vlastnosti GIF

Graphics Interchange Format
Používá bravenou paletu (256 položek)
Obrázek je tvořen rámci
Součástí každého rámce je:
- Souřadnice levého horního rohu, šířka a výška
- Volitelně lokální barevná paleta
- Obrazová data komprimována pomocí LZW
Může obsahovat animace, kdy každý rámec obsahuje jeden snímek animace (každý rámec má nastaveno zpoždění)
Jednobitový alfa kanál (jedna barva v paletě je úplně průhledná)

GIF & Web

Barevnost GIF obrázků

Kolik různých barev může obsahovat obrázek uložený pomocí formátu GIF?

V GIFu může být uložen plněbarevný obrázek, protože obraz může být rozdělen na více rámců s vlastní lokální barevnou paletou.

Jak je to s barevností a efektivností animovaných gifů?

Je to neefektivní pralesní technologie! Na animace použijte element HTML5 <video>

GIF a průhlednost

PNG

“No software patents, please!”

Vlastnosti PNG

Portable Network Graphics
Stupňě šedi
Barevná paleta (24 bitová)
RGBA (32bpp)
Umožňuje použít až 16 bitů na jeden kanál
Komprese DEFLATE

PNG a průhlednost

JFIF

“My name is JFIF not JPEG!”

Vlastnosti JFIF

JPEG File Interchange Format
RGB (24bpp)
JPEG kompresní formát
EXIF data
- Meta informace o daném obrázku
- Doba vzniku
- Jaký program/zařízení daný obrázek vytvořil
- GPS souřadnice
- A spoustu dalších

JFIF & Web

5% (6KB)

50% (29KB)

95% (151KB)

TIFF

“So complicated!”

Vlastnosti TIFF

Funkčně velmi bohatý formát. Je možné vytvářet vlastní rozšíření. Ve výsledku ho žádný program nepodporuje plně.

WebP

“Designed for web!”

Vlastnosti WebP

Vytvořen firmou Google v roce 2010 z video formátu WebM a RIFF
Podporuje jak ztrátovou tak bezeztrátovou kompresi. Při použití ztrátové komprese lze dosáhnout o 30% lepšího kompresního poměru oproti klasické JPEG kompresi.
Podporuje průhlednost
Podporuje jednoduché animace
Podpora v aplikacích zatím slabší. Z prohlížečů zatím Google Chrome a Opera.

WebP (lossy) & Web

WebP (animated) & Web

WebP (alpha) & Web

Bezeztrátová komprese

Ztrátová komprese

OpenEXR

“I said high tech, yeah!”

Obrazy s vysokým dynamickým rozsahem

V případě, že chceme rozlišit velký rozsah jasových hodnot (bílý papír, svíčka, žárovka, zářivka, slunce), tak rozsah < 0, 255 > nestačí a je nutné použí rozsah < 0.0, FLOAT_MAX >

Vyžití takových obrázků není pouze v nasvětlování scény, ale hlavní využití je predevším ve filmové postprodukci.

Problematické je zobrazení na běžných monitorech (rozsah hodnot < 0, 255 >)

Lokální mapování tónů

Vlastnosti OpenEXR

Vytvořen v grafickém studiu ILM
Vysoký dynamický rozsah
Podpora pro vrstvy
Podpora pro několik bezeztrátových kompresních formátů
Umožňuje ukládat i další data důležitá v postprodukci (hloubku obrazu, rychlost fragmentů, apod.)
Open Source

Vektorové souborové formáty

Vektorová grafika

Kvalita obrázků je nezávislá na zvětšení (problémem může být příliš velké zmenšení)
Obraz není tvořen rastem, ale je vytvořený ze základních primitiv:
- Úsečka, obdelník, elipsa, Bézierova křivka, text, barevné přechody, lze použít i rastrovou texturu.

SVG

“Size does not matter!”

Vlastnosti SVG

Specifikováno W3C
Textový formát založený na XML
Filtry (např: rozostření)
Podpora pro animace
Možné stylovat pomocí CSS (v současné době plně pouze Firefox)
Dobrá podpora napříč prohlížeči

Příklad SVG

SVG & Web

SVG (animace) & Web

Grafický software