Reprezentace 3D objektů
Kurz počítačové grafiky
Autor: Jiří Hnídek / jiri.hnidek@tul.cz
Základní dělení
- Hraniční reprezentace
- Plošková reprezentace
- Bodová reprezentace
- Konstruktivní geometrie těles
- Objemová reprezentace
Plošková reprezentace
Nejčastější způsob uložení 3D objektů v paměti i na disku. Nezajímá nás vnitřek objektu, ale pouze to, co je na povrchu.
Povrch je složen z:
- Vertexy (3D souřadnice krajních bodů)
- Hrany (spojení dvou vertexů)
- Plošky (spojení alespoň tří vertexů)
Trojúhelník & N-úhelník
Síť n-úhelníků se nakonec v zobrazovacím řetězci vždy převádí na śíť trojúhelníků, protože trojúhelník má několik důležitých vlastností.
- Všechny jeho body leží v jedné rovině.
- Trojúhelník je vždy konvexní.
- Lze jednoduše a jednoznačně spočítat jeho normálový vektor z jeho krajních bodů.
- Lze jednoduše provádět jeho rasterizaci.
Síť trojúhelníků
Síť trojúhelníků i libovolných n-úhelníků má vždy dvě části:
Geometrická struktura
- Obsahuje pouze souřadnice vertexů
Topologická struktura
- Obsahuje informace o tom, jak jsou vertexy pospojovány do hran a plošek.
Optimalizace sítě trojúhelníků
Síť je někdy vhodné převést na pruh trojúhelníků nebo vějíř trojúhelníků
- Není nutné přenášet takové množství dat na grafický akcelerátor
- Nutná podpora na grafickém akcelátoru a použitém API (OpenGL, WebGL, atd.)
Manifoldní a non-manifoldní objekty
Manifoldní objekt je tzv. vyrobitelný objekt a jeho topologická struktura musí splňovat následující 3 podmínky:
- Každá hrana musí být sdílena pouze dvěma ploškami.
- Žádná hrana neprotíná jinou plošku.
- Žádný vertex nespojuje dvě části objektu.
Jednoduchá plošková reprezentace těles
- Předpokladem je uložení objektu, který splňuje alespoň některá kritérie pro manifoldní objekt.
- Obsahuje informace pouze o poloze vertexů a jejich propojení do plošek.
- Tato struktura je vhodná pro uložení do souboru, případně paměti.
- Je hrubě nevhodná pro úpravu geometrické/topologické struktury.
Příklad - Krychlička
4+----+7
/| /|
5+----+6|
| | | |
|0+--|-+3
|/ |/
1+----+2
Příklad sítě trojúhelníků
Geometrická struktura - vetexy
| 0.0, 0.0, 0.0 | 1.0, 0.0, 0.0 | 1.0, 1.0, 0.0 | 0.0, 1.0, 0.0 | 0.0, 0.0, 1.0 | 1.0, 0.0, 1.0 | 1.0, 1.0, 1.0 | 0.0, 1.0, 1.0 |
Topologická struktura - plošky
| 0, 3, 2, 1 | 0, 1, 5, 4 | 1, 2, 6, 5 | 2, 3, 7, 6 | 3, 0, 4, 7 | 4, 5, 6, 7 | 4, 5, 9, 8 |
Normálový vektor
Normálový vektor plošky lze jednoznačně spočítat ze souřadnic krajních vertexů.
Když budeme uvažovat trojúhelník s krajními body: $P_{1} = [x_{1}, y_{1}, z_{1}]$, $P_{2} = [x_{2}, y_{2}, z_{2}]$ a $P_{3} = [x_{3}, y_{3}, z_{3}]$, tak normálový vektor $\vec{n}$ můžeme spočítat pomocí:
$$ \vec{v_{21}} = P_{2} - P_{1}; \quad \vec{v_{32}} = P_{3} - P_{2} \\ \vec{n} = \vec{v_{21}} \vec{v_{32}} $$Datová struktura okřídlené hrany
- Datová struktura vhodná pro dynamickou úpravu geometrie a topologie.
- Lze ji použít pouze pro uložení manifoldních objektů.
- Obsahuje jednak geometrickou strukturu (vertexy).
- Většina informací o topologii je uložena na hranách.
- Dva odkazy na oba vertexy
- Dva odkazy na sousedící plošky
- Čtyři odkazy na přilehlé plošky
- Ploška obsahuje pouze odkaz na jednu ze svých hran.
Příklad okřídlené hrany
| $E_{1}$ | |
| $V_{1}$ | $V_{2}$ |
| $F_{1}$ | $F_{2}$ |
| $E_{3}$ | $E_{4}$ |
| $E_{2}$ | $E_{5}$ |
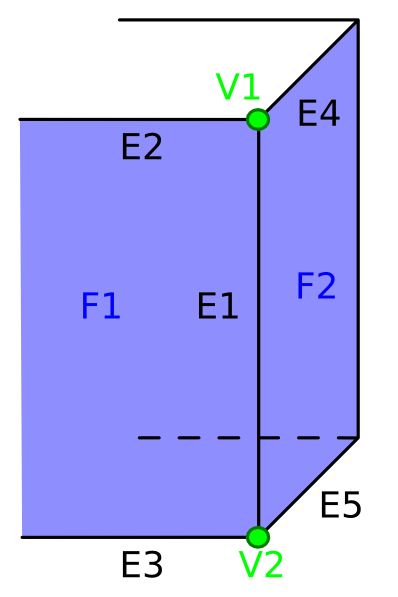
Vlastnosti okřídlených hran
- Lze jednoduše nalézt všechny sousední plošky
- Lze jednoduše nalézt smyčku hran/plošek
- Ploška nemusí být konvexní
- Ploška může obsahovat díry
Datová struktura půlhrany
- Odstraňuje omezení okřídlených hran na manifoldní objekty.
- Každá hrana je rozdělena na N "půlhran".
Vlastnosti vertexů, hran, plošek a rohů plošek
V aplikacích běžně potřebujeme ukládat společně s geometrickou a topologickou strukturou další dodatečné informace.
Způsob uložení takových dat se liší v závislosti na využití objektů.
Je možné ukládat další uživatelem definované informace.
Vlastnosti vertexů
- Váha vertexů (viz. dopředná a inverzní kinematika)
- Barva vertexů
Vlastnosti hran
- Ostrost hran
- UV mapování ("šev")
Vlastnosti plošek
- Typ stínování
- Textura
- Barva
Vlastnosti rohů plošek
- UV souřadnice
- Barva
Dělené plošky
- Algoritmus, který vyhlazuje povrch tělesa s ploškovou reprezentací.
- Existuje několik dělících schémat (aproximační a interpolační).
- Nejčastěji se používá dělící schéma: Catmull-Clark
- Rekurzivní algoritmus
- Generuje čtvercovou síť.
- Výsledná ploch má spojitost $C^{2}$
Dělící schéma Catmull-Clark
Výsledná plocha jedné iterace je tvořena ploškovými, hranovými a vrcholovými vertexy.
Ploškový vertex $V_{F_{i}}$ je průměrem všech vertexů tvořící danou plošku $F_{i}$.
Hranový vertex se spočítá podle následujícího vztahu:
$$ V_{E} = \frac{E_{1} + E_{2} + V_{F_{1} + V_{F_{2}}}}{4} $$Vrcholový vertex se spočítá podle následujícího vztahu:
$$ V_{V} = \frac{1}{N}(\frac{1}{N}\sum_{i=1}^{N}V_{F_{i}} + \frac{1}{N}\sum_{i=1}^{N}V_{E_{i}} + \frac{(N-3)}{N}V) $$kde $V$ je půvdní vertex
Transformace objektů
Stejně jako v případě 2D transformací i ve 3D se transformace objektů (posun, rotace, atd.) realizují pomocí transformačních matic a homogenních souřadnic:
$$ \begin{align} X' &= \frac{X}{w} \\ Y' &= \frac{Y}{w} \\ Z' &= \frac{Z}{w} \\ \end{align} $$Transformační matice
Obecná transformační matice pro 3D transformace má následující tvar:
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} m_{1,1} & m_{1,2} & m_{1,3} & m_{1,4} \\ m_{2,1} & m_{2,2} & m_{2,3} & m_{2,4} \\ m_{3,1} & m_{3,2} & m_{3,3} & m_{3,4} \\ m_{4,1} & m_{4,2} & m_{4,3} & m_{4,4} \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Posun
Posun můžeme vyjádřit vektorem posunutí $(dx, dy, dz)$ a maticovým násobením:
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & dx \\ 0 & 1 & 0 & dy \\ 0 & 0 & 1 & dz \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Kontrolní otázka: Je posunutí lineární transformace?
Nikoliv! Poloha není lineární kombinací původních souřadnic. Na posunutí můžeme pohlížet jako na zkosení ve čtyřrozměrném prostoru.
Zvětšení/zmenšení
Zvětšení nebo zmenšení může být ve směru os různé a je vztažené vůči počátku soustavy souřadné:
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} S_{x} & 0 & 0 & 0 \\ 0 & S_{y} & 0 & 0 \\ 0 & 0 & S_{z} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Kontrolní otázka: Jak by vypadala transformační matice pro zrcadlení vůči rovině XZ?
Odpověď: $S_{x} = 1, S_{y} = -1, S_{z} = 1$
Zkosení
Zkosení ve směru jedné osy. V tomto případě ve směru osy x
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} 1 & s_{x} & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Otočení (kolem osy Z)
Transformační matice pro otočení není tak triviální jako ve 2D. Transformace se opět provádí vůči počátku soustavy souřadné kolem osy, ale je nutné určit kolem jaké osy otočení provádíme.
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 & 0 \\ \sin\gamma & \cos\gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Otočení (kolem osy X)
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Otočení (kolem osy Y)
$$ \begin{bmatrix} X' \\ Y' \\ Z' \\ w' \\ \end{bmatrix} = \begin{bmatrix} \cos\beta & 0 & -\sin\beta & 0 \\ 0 & 1 & 0 & 0 \\ \sin\beta & 0 & \cos\beta & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ w \\ \end{bmatrix} $$Otočení - pořadí transformací
Je zřejmé, že pro obecné ototčení záleží na tom v jakém pořadí se jednotlivé parciální transformace otočení provádí. Tím se myslí, jestli se nejprve provede otočení vůči ose X, následně otočení vůči ose Y a nakonec vůči ose Z.
Různé aplikace i API mohou mít různé pořadí a konvence.
Z tohoto důvodu je vhodné kromě úhlů otočení $(\alpha, \beta, \gamma)$ uvádět i pořadí jednotlivých otočení, např.: XYZ, ZXY, atd.
Rotace vyjádřené pomocí úhlů a pořadí operací se také špatně skládají a interpolují.
Otočení - Kvaterniony (Quaternions)
Z důvodu z míňěné výše se často používá matematický aparát nazývaný kvaterniony.
Kvaterniony trochu připomínají komplexní čísla
Kvaternion obsahuje hned 3 "imaginární" složky:
kde $w, x, y, z$ jsou reálná čísla a $i, j, k$ jsou kvaternionové jednotky.
Kvaterniony - základní pravidla
Kvaterniony mají definováno několik základních pravidel:
$$ i^{2} = j^{2} = k^{2} = ijk = -1; $$ $$ ij = -ji = k, jk = -kj = i, ki=-ik = j $$Někdy se kvaterniony vyjadřují pomocí:
$$ q = (s, \vec{v}) $$,kde $s$ je skalární část a $\vec{v}$ je vektorová část
Sdružený kvaternion
Ke kvaternionu $q = w + ix + jy + kz$ definujeme kvaternion sdružený:
$$ q^{*} = w - ix - jy - kz $$Velikost kvaternionu spočítáme pomocí:
$$ |q| = \sqrt{w^{2} + x^{2} + y^{2} + z^{2}} $$Kvaternion, jehož velikost je jedna se nazývá jednotkový kvaternion a platí pro něj:
$$ |q| = 1; \quad q^{*}q = qq^{*} = 1 $$Rotace vyjádřená kvaterniony
Rotaci o úhel $\alpha$ kolem vektoru $\vec{v} = (v_{x}, v_{y}, v_{z})$ lze vyjádřit pomocí:
$$ q = \cos(\alpha/2) + v_{x}\sin(\alpha/2)i + v_{y}\sin(\alpha/2)j + v_{z}\sin(\alpha/2)k $$Rotace pomocí kvaternionu
Mějme bod $P = [p_{x}, p_{y}, p_{z}]$, a jeho polohový vektor $\vec{p} = (p_{x}, p_{y}, p_{z})$ můžeme chápat jako kvaternion s nulovou skalární částí. Otočení vektoru $\vec{p}$ kolem vektoru $\vec{v}$ o úhel $\alpha$ můžeme vyjádřit jako:
$$ \vec{p}' = q v q^{*} $$Další informace o kvaternionech naleznete v monografii Moderní počítačová grafika na str. 549.